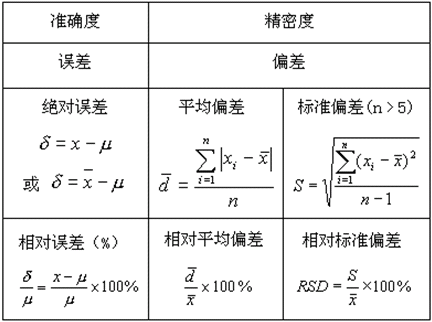
1。知识点的定义和解释:相对-2偏差是一个统计指标,用来衡量一个数据集中每个数据的离散程度及其平均值。它可以帮助我们判断数据的可变性或误差。通常标准 偏差除以平均值得到相对的标准 偏差。2.知识点应用:相对-2偏差可以帮助我们比较不同数据集之间的离散度。常用于质量控制、经济研究、实验结果评价等领域。3.知识点举例说明:例题:计算下列数据集的相对-2偏差:答案:首先我们需要计算数据集的平均值和-2偏差。平均值的解法:(10 12 15 18 20)/515。标准偏差解法:先计算各数据与平均值之差的平方和的平均值,然后开方。差的平方和的平均值:标准 StandardDeviation,在概率统计中最常用作统计离差的度量。标准差定义为方差的算术平方根,它反映了群体中个体之间的分散程度。原则上,衡量分布程度的结果有两个性质:标准一个总数的差或标准一个随机变量的差,和标准一个子集中样本数的差。公式如下。
第一步,这里计算平均值(A1 A2 An)/n,5和9的平均值为(5 6 8 9)/47。第二步,计算标准差标准差σ √ 0.25 * {(553。存在标准总体的差异或标准随机变量的差异和标准样本子集的差异。
(1015)^2 (1215)^2 (1515)^2 (1815)^2 (2015)^2]/5(25 9 0 9 25)/518. 标准 偏差:√18≈4.2426.最后,使用相对 标准 偏差的公式,用 标准 偏差除以平均值。
/image-6/[6、什么叫 标准差? 标准差的计算公式?Solution:S1/6×[(8077) (8078) (8079) (8081) (8082) (8083)]。1/6×(9 4 1 1 4 9)。1/6×28。14/3。标准差:S根号42/3。标准 StandardDeviation,即偏离均方的算术平均值(即方差)的算术平方根,用σ表示。标准差也叫标准 偏差,或实验 标准差,在概率统计中最常用作统计分布的度量依据。
标准差异可以反映一个数据集的离散程度。两组数据平均值相同,标准差值可能不相同。离差:标准差是最常用的反映一组数据离散程度的量化形式,是衡量准确性的重要指标。说到标准区别,首先要明白它的目的。我们用方法检测它,但是检测方法总是有误差的,所以检测值不是它的真值。检测值与真实值的差距是评价检测方法最具决定性的指标。
7、请问 标准差怎么计算?标准差:是偏离均方的算术平均值(即方差)的算术平方根,用σ表示。标准差也叫标准 偏差,或实验 标准差,在概率统计中最常用作统计分布的度量依据。人口标准差:和方差:方差标准差的平方。在实验中,单次测量不可避免的会产生误差,所以我们往往会多次测量,然后用测量值的平均值来表示被测量的量,用误差棒来表征数据的分布,其中误差棒的高度为 标准error。
{10}
8、 标准差怎么算出来的1,sample标准偏差:2,population标准偏差:population标准。sample标准偏差,又称实验标准偏差:从总体中抽样,用样本计算总体-。扩展数据的差异标准可以反映一个数据集的离散度。标准 偏差越小,这些值偏离平均值越小,反之亦然。标准 偏差可以用标准 偏差与平均值的比值关系来度量。
{11}
例如,A组和B组的六名学生参加了相同的语文考试。A组的得分为95、85、75、65、55和45,B组的得分为73、72、71、69、68和67。这两组的平均值都是70,但是A组的标准之差应该是17.078,B组的标准之差应该是2.160,可见A组学生之间的差距比B组要大得多。
{12}
9、 标准 偏差怎么求?标准差值计算公式:标准差值σ方差平方。标准difference(standard deviation),数学术语,是偏离均方的算术平均值(即方差)的算术平方根,用σ表示。标准差也叫标准 偏差,或实验 标准差,在概率统计中最常用作统计分布的度量依据。标准 Difference是方差的算术平方根。标准差异可以反映一个数据集的离散程度。两组数据平均值相同,标准差值可能不相同。
标准差的定义是标准的值与其均值的偏差的平方的算术平均值的平方根。它反映了群体中个体之间的分散程度,测量分布程度的结果原则上有两个性质:它是非负值,与测量数据具有相同的单位。存在标准总体的差异或标准随机变量的差异和标准样本子集的差异,简单来说,标准差是一组数据的离散程度的度量。标准相差较大,表示大部分数值与其平均值相差较大;标准的微小差异意味着这些值更接近平均值。







